
レンズの明るさを示す絞り値、Fナンバーは、2.8、4.0、5.6といった数字になっています。
カメラは人が作った道具なので、レンズのF値の数字も何か理由があってそのような数字にしているものと思われます。
ここではF値がキリが良いように思えない数値になっている理由について、数学や工学が得意というわけではない当ブログ運営者の私が自分で理解しやすいような素人らしい計算をしてみて、おおまかな雰囲気をご紹介します。
レンズの口径比やF値などのおおまかな定義など
口径比、焦点距離、F値
下図のように、口径が \(D\) で、焦点距離が \(f\) 、のレンズを通って光がフィルムにあたって照度 \(E\) の明るさになっているとします。
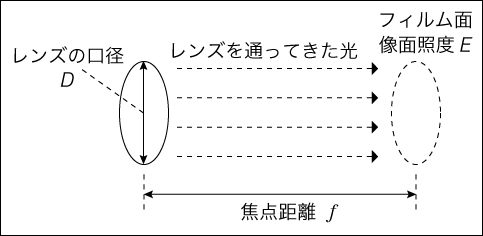
カメラを単純化した図
口径比は \(\frac{D}{f}\)
\(\frac{D}{f}\) の分子と分母に \(\frac{1}{D}\) をかけて \(\frac{1}{\frac{f}{D}}\)
\(\frac{1}{\frac{f}{D}}\)を比で表して \(1:\frac{f}{D}\)
\(\frac{f}{D}=\rm{Fno}\)と書いてみると \(1:\rm{Fno}\)
\(\rm{Fno}\)がFナンバーです。
像面照度Eを表してみる
レンズを通った光がフィルムにあたっている場所の照度Eを表してみます。
フィルムに光があたっている場所の照度は、口径 \(D\) のレンズの面積に比例し、焦点距離の2乗に反比例する、ということが知られているので、そのことを式で表してみます。
\[
E=k\pi\left(\frac{D}{2}\right)^{2}\cdot\frac{1}{f^2}
\]
さらに計算して形を変えて
\[\begin{align}
E&=k\pi\left(\frac{D}{2}\right)^{2}\cdot\frac{1}{f^{2}}\\
&=k\pi\frac{D^{2}}{4}\cdot\frac{1}{f^{2}}\\
&=\frac{\pi k}{4}\cdot\left(\frac{D}{f}\right)^{2}
\end{align}\]
\(K=\frac{\pi k}{4}\)とすると
\[\begin{align}
E&=K\cdot\left(\frac{D}{f}\right)^2\\
&=K\cdot\frac{D^2}{f^2}\\
&=\frac{K}{\frac{f^2}{D^2}}\\
&=\frac{K}{\left(\frac{f}{D}\right)^2}
\end{align}\]
\(\frac{f}{D}=\rm{Fno}\)なので
\[
E=\frac{K}{\left(\rm{Fno}\right)^2}
\]
像面照度が変化したときのF値の変化をみてみる
レンズの明るさを変える主な目的は、入ってくる光を調節して結果としてフィルムに光が当たっている場所の明るさを変化させることでしょう。
そこで、フィルムに光が当たっている場所である像面の照度を、キリが良いように2分の1にしてみたとき、F値はどのように変化するかみてみます。
先ほど導いた式を、\(\rm{Fno}\) を求める形に変えます。
\[\begin{align}
E&=\frac{K}{\left(\rm{Fno}\right)^2}\\
E\left(\rm{Fno}\right)^2&=K\\
\left(\rm{Fno}\right)^2&=\frac{K}{E}\\
\rm{Fno}&=\sqrt{\frac{K}{E}}
\end{align}\]
像面照度 \(E\) に \(\frac{1}{2}\) をかけてみます。
\[\begin{align}
\sqrt{\frac{K}{E\cdot\frac{1}{2}}}&=\sqrt{\frac{K}{\frac{E}{2}}}\\
&=\sqrt{\frac{2K}{E}}\\
&=\sqrt{2}\sqrt{\frac{K}{E}}
\end{align}\]
この式から分かる通り、\(E\) に \(\frac{1}{2}\) をかけて照度を半分にしてみた結果、元の \(\rm{Fno}\)の \(\sqrt{2}\) 倍になりました。
照度を1/2にするとF値がルート2倍になった
\(E\) に \(\frac{1}{2}\) をかけて照度を半分にしてみた結果、元の \(\rm{Fno}\) の \(\sqrt{2}\) 倍になりました。
計算は省略しますが、逆に \(E\) を2倍にすると、\(\rm{Fno}\) は \(\frac{1}{\sqrt{2}}\) 倍になりました。
F値はルート2倍ずつの区切りになっている
\(E\) を半分にすると \(\rm{Fno}\) が \(\sqrt{2}\) 倍になったので、逆に言うとF値を \(\sqrt{2}\) 倍にすると照度 \(E\) が \(\frac{1}{2}\) になるということです。
F値を \(\sqrt{2}\) 倍ずつ変化させると、像面照度がキリ良く2倍ずつ変化します。
そのためカメラのF値は1、1.4、2.0、2.8、4.0、5.6、8.0、…といった具合に、\(\sqrt{2}\) 倍ずつの数値になっています。
このページの説明は高校時代に勉強についていけなくなり落ちこぼれてほぼオール赤点で学校からは人間扱いもされていなかった当ブログ運営者が自分で理解できるように書いてみたもので、素人らしい説明になっています。
専門書には秩序立てた説明が載っており、Fナンバーを \(\sqrt{2}\) 倍系列にすることで、像面照度が2の倍数系列になる、といったことが書かれています。
以上、F値がキリが良いように思えない数値になっている理由について、数学や工学が得意というわけではない当ブログ運営者の私が自分で理解しやすいような素人らしい計算をしてみて、おおまかな雰囲気をご紹介しました。
参考書籍



