カラーマネジメントは、色に関する仕組みです。
色を細かく正確に管理するためには、色を数値で表す必要があります。
色彩工学の専門書などに、色を数値で表す方法の秩序立てた説明が載っています。
ここでは、どのようにして色を数値で表すのか、おおまかな雰囲気をご紹介します。
色とは何か
色は光が目に入った結果生じる感覚
雰囲気で言えば、色は光が人の目に入ってその結果人に生じる感覚です。
光は色々な波長の電磁波が混ざったもの
人に色を感じさせる光の正体は電磁波です。
電磁波の中でも、人の視覚でとらえることのできる範囲の波長の電磁波のことを光と呼んでいます。
私たちが通常見ている光は、たいてい何種類もの波長の電磁波が混ざっています。
目に入る光の波長が違えば、違う色に見えたりする
全く同じ波長の光なら、目で見ると同じ色に見えます。
波長が違う光は、目で見ると違う色に見えます。
色々な波長が混ざっている光の場合、混ざり具合が異なれば違う色に見えることもあれば、同じ色に見える場合もあります。
色を数値で表すため、色を感じさせる原因である光を数値で表してみる
色を感じさせる原因である光を数値で表してみます。
光の強さを測る方法は色々あります。他の書籍等をご参照ください。
光はたいていの場合色々な波長の光が混ざっているので、光の中の各波長の光がどのくらいの強さか測ってみます。
その結果、光を分光強度分布というもので表せます。
光の成分である各波長の光がどのくらい強いかを表したものです。
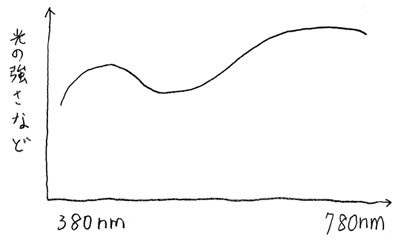
分光強度分布
分光強度分布だけでは色を表したことにならない
色を感じさせる原因である光の分光強度分布を表せれば、色を数値で表せたも同然のような気がします。
ところが光の分光強度分布を表しただけでは、色を数値で表したことにはなりません。
違う光でも、人の目には同じ色に見えることがある
色は光そのものではなく、光が人の目に入った結果感じる感覚です。
分光強度分布が異なる光A、光Bをそれぞれ人が見た時、分光強度分布が異なるにも関わらず人の目には同じ色に感じるという場合があります。
分光強度分布=色を数値で表したもの ということにはならない
分光強度分布が異なっても同じ色に見えるという例もあるので、単純に光を数値にしても色を数値化したことにはなりません。
詳しくは他にも色々ありますが、色を数値で表すためには分光強度分布を単純に使うわけにはいかず、さらに工夫がいります。
色を数値で表す仕組みの大まかな雰囲気
色は人の感覚なので、実際に人が色を見る実験をしてみる
光の分光強度分布が単純に色を数値化したものということにはできないことが分かりました。
そこで、色は光が人の目に入った結果生じる感覚なので、色々な光が人にどう見えるか実験して数字で記録してみます。
色々な色を見る実験をするというと、色は無限にあってキリがなさそうに感じます。
しかし、光は人の視覚でとらえることができる波長域の電磁波であり、無限にあるわけでなく波長の範囲が限られているので、方法を工夫して根気良く実験するとそのうち終わります。
単波長の光と、RGBの各光を混ぜたものが、同じ色に見えるように調節してみる
例えば波長600nmの単波長の光と、波長700nm(赤っぽい光)・波長546.1nm(緑っぽい光)・波長435.8nm(青っぽい光)の3種類の単波長の光を混ぜた光、を同時に見ます。
赤・緑・青の光の強さをそれぞれ調節して、600nmの光と同じ色に見えるようにしてみます。
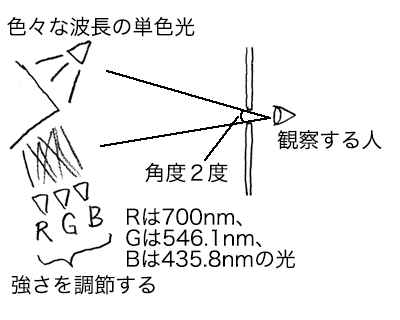
単波長の光と、3つの単波長の光を混ぜた光が同じに見えるようにする実験
同じことを、
波長380nmの光と赤・緑・青を混ぜた光、
波長385nmの光と赤・緑・青を混ぜた光、
波長390nmの光と……
というように、380nm前後〜780nm前後の単波長の光について行います。
その結果、各単波長の光と、それと同じ色に見える赤・緑・青の光の強さの組み合わせが分かります。
おおまかに言うと、この組み合わせの表を等色関数といいます。
判明した等色関数を使えば色を数値で表せる
以上の説明のように実験をして等色関数が分かれば、色々な色を数字で表せます。
上記の実験では単波長の光の場合しか実験していないので、太陽や照明など通常目にする色々な波長の光が混ざっている光の色は表せないではないか、と思うかもしれません。
ところが、単波長の光と赤・緑・青の光の釣り合いの結果さえ一通り分かれば、その結果の足し算や引き算などの計算をすることで複数の波長の混ざった光も表すことができます。
どのように計算するのかなど、詳しくは色や光に関する専門書と高校の頃の数学の教科書などをご参照ください。
上記の色の数値表現を、使い勝手が良くなるように用途により変換などをする
上記の説明のような方法により色を数値で表す基礎はできました。
実際には、この表現をより使い勝手が良いように座標を変換したり、観察条件を変えたり、明るさの要素の扱い方を工夫したり、色々な方法により工夫を加えて、色を表すための単位系である「表色系」が作られています。
例えば、よく目にするCIELAB均等色空間などです。
万能の表色系が作れないため、表色系は何種類も存在し、用途によって使いやすい表色系を選びます。
参考書籍
色を数値で表す方法に関する秩序立てた正確な説明は、色彩工学などの分野の専門書に載っています。
以上、どのようにして色を数値で表すのかについて、おおまかな雰囲気をご紹介しました。
参考記事